Colegio de bachilleres del estado de Tlaxcala plantel
03
Nombre del alumno: Elizabeth García Pérez
Materia: calculo
Grupo: 613
Profesor: Rosendo
Jiménez ortega
Turno: vespertino
INTRODUCCION
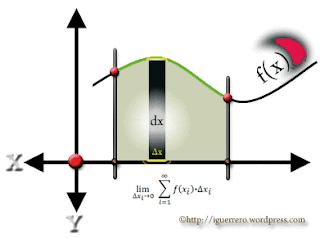
La idea del cálculo integral consiste en calcular, en general, superficies curvilíneas, es decir, el área entre la gráfica de una función y el eje-x.
Estamos de acuerdo con la siguiente notación:

La cuadratura de la parábola discutida en nuestra última sección constituye, quizás, el primer descubrimiento del joven Arquímedes y es, en sí mismo, un acontecimiento revolucionario. Su significado pleno sólo pudo ser apreciado gradualmente. Arquímedes presenta dos pruebas geométricas de este hecho, una con un paralelogramo y otra con un rectángulo. Siguiendo este último método Cavalieri (en 1630) logra "cuadrar" parábolas de la forma no sólo y = x2, como es el caso de Arquímedes, sino y = x3, y = x4, y = x5,..., y = xk, hasta k = 9. En cada caso, respectivamente, obtuvo los valores: 1/4, 1/5, 1/6 ...y 1/10 para k = 9. Concluyó, como era de esperarse, que para k =10 obtendría 1/11. Pero no. Esta fórmula presentó un problema nuevo que ya no pudo manejar. El resultado general cuando k es un entero arbitrario fue obtenido por Fermat alrededor de 1650.




La integral del enunciado puede resolverse haciendo el cambio :

con lo que nos queda :

La fiesta de las f(x)'s (Funciones de X)
Estamos de acuerdo con la siguiente notación:

Es la integral definida de la función f de [variable] x [los límites] de A a B. Se pretende que la zona entre la curva y los ejes como en la imagen de arriba S. Más específicamente, es que esta es una integral de Riemann (por ejemplo, Riemann), hay también integrante líneas generales.
El cálculo integral se refiere al cálculo de integrales tales.
El cálculo integral se refiere al cálculo de integrales tales.
DESARROLLO El origen del cálculo integral se
remonta a la época de Arquímedes (287-212 a.C.), matemático griego de la
antigüedad, que obtuvo resultados tan importantes como el valor del área
encerrada por un segmento parabólico. La derivada apareció veinte siglos
después para resolver otros problemas que en principio no tenían nada en común
con el cálculo integral. El descubrimiento más importante del cálculo
infinitesimal (creado por Barrow, Newton y Leibniz) es la íntima relación entre
la derivada y la integral definida, a pesar de haber seguido caminos diferentes
durante veinte siglos. Una vez conocida la conexión entre derivada e integral
(teorema de Barrow), el cálculo de integrales definidas se hace tan sencilla
como el de las derivadas.
El
concepto de Cálculo y sus ramificaciones se introdujo en el siglo XVIII, con el
gran desarrollo que obtuvo el análisis matemático, creando ramas como el
cálculo diferencial, integral y de variaciones.
El cálculo
diferencial fue desarrollado por los trabajos de Fermat, Barrow, Wallis y
Newton entre otros. Así en 1711 Newton introdujo la fórmula de interpolación de
diferencias finitas de una función f(x); fórmula extendida por Taylor al caso
de infinitos términos bajo ciertas restricciones, utilizando de forma paralela
el cálculo diferencial y el cálculo en diferencias finitas. El aparato
fundamental del cálculo diferencial era el desarrollo de funciones en series de
potencias, especialmente a partir del teorema de Taylor, desarrollándose casi
todas las funciones conocidas por los matemáticos de la época. Pero pronto
surgió el problema de la convergencia de la serie, que se resolvió en parte con
la introducción de términos residuales, así como con la transformación de
series en otras que fuesen convergentes. Junto a las series de potencias se
incluyeron nuevos tipos de desarrollos de funciones, como son los desarrollos
en series asintóticas introducidos por Stirling y Euler. La acumulación de
resultados del cálculo diferencial transcurrió rápidamente, acumulando casi
todos los resultados que caracterizan su estructura actual
Introducir
el cálculo integral, se logro con el estudio de J.Bernoulli, quien escribió el
primer curso sistemático de cálculo integral en 1742. Sin embargo, fue Euler
quien llevó la integración hasta sus últimas consecuencias, de tal forma que
los métodos de integración indefinida alcanzaron prácticamente su nivel actual.
El cálculo de integrales de tipos especiales ya a comienzos de siglo, conllevó
el descubrimiento de una serie de resultados de la teoría de las funciones
especiales. Como las funciones gamma y beta, el logaritmo integral o las
funciones elípticas.
La cuadratura de la parábola discutida en nuestra última sección constituye, quizás, el primer descubrimiento del joven Arquímedes y es, en sí mismo, un acontecimiento revolucionario. Su significado pleno sólo pudo ser apreciado gradualmente. Arquímedes presenta dos pruebas geométricas de este hecho, una con un paralelogramo y otra con un rectángulo. Siguiendo este último método Cavalieri (en 1630) logra "cuadrar" parábolas de la forma no sólo y = x2, como es el caso de Arquímedes, sino y = x3, y = x4, y = x5,..., y = xk, hasta k = 9. En cada caso, respectivamente, obtuvo los valores: 1/4, 1/5, 1/6 ...y 1/10 para k = 9. Concluyó, como era de esperarse, que para k =10 obtendría 1/11. Pero no. Esta fórmula presentó un problema nuevo que ya no pudo manejar. El resultado general cuando k es un entero arbitrario fue obtenido por Fermat alrededor de 1650.
No obstante, ¿era necesario suponer que
k es un entero? Cuando k no es un entero -usando notación moderna- el problema
equivale a encontrar la derivada de la función
y = xn,
en x = 1.
La Invención
del Cálculo
Haremos, en lo que sigue, un poco de
historia, más que por la historia misma, con la intención de iluminar el
desarrollo del pensamiento matemático. Independientemente de su historia, las
verdades matemáticas son inmutables y el organizar estas verdades en
nuestras mentes, nuestra relación con ellas y el uso que hacemos de las mismas
puede en realidad afectarse al reconocer su adecuado ordenamiento en el tiempo.
Dijimos que Fermat conoció algunas partes del cálculo diferencial así como
soluciones de ciertos problemas inversos. Supo también de algunas integrales.
Por su parte, Gregorio San Vicenzo descubrió relaciones entre integrales y
funciones que, si bien no fueron notadas sino hasta después de su publicación,
involucraban las propiedades de los logaritmos.
En el origen del concepto de número,
además de las matemáticas griegas, las cuales eran geométricas en forma, se
desarrollaron las matemáticas computacionales de los hindúes y los babilonios y
durante la edad media, por la época en que los arábes eran los
el concepto más amplio posible de una
función diferenciable. Dada una expresión puramente computacional, se puede
incursionar con seguridad en el campo de los diferenciales; este fue el
desarrollo que se estableció en 1640. Gregorio San Vicenzo y Christiaan Huygens
todavía pensaban a la manera de los griegos antiguos; Barrow se vio atrapado
por la corriente del concepto de función computacional y trató de ajustarlo al
modo de pensar griego. Newton nació pocos años después de Barrow pero pertenecía
a la nueva generación de la expresión computacional. Es extraño el significado
que hay por el año de su nacimiento. De hecho, reconocer el significado de
"las generaciones", que debemos a la historia del arte, es de suma
importancia para entender la historia de las matemáticas. El caso anterior es
un ejemplo notable de ello. Lo que Newton absorbió desde el principio
permaneció ajeno a Barrow por el resto de su vida: el giro del concepto de
función geométrica al de función computacional; el giro de los confines del
arte griego de la prueba a la fácil flexibilidad de los indivisibles. En una
página de su trabajo Barrow alude brevemente a estos asuntos pero, rápidamente,
como si estuviera horrorizado, los deja de nuevo. De aquí que la línea
fronteriza que lo separa de sus sucesores, resida en la distribución del
énfasis. Cierto es que Barrow descubrió el teorema fundamental pero, ¿qué hizo
con el? En principio se pueden hacer dos cosas con él: podemos usar integrales
definidas conocidas como
b
ó õ a |
xndx
|
para derivar de ellas integrales
indefinidas
ó õ |
xndx
|
EJEMPLO
con lo que nos queda :
La integral dada en el enunciado puede resolverse realizando el cambio :

y a partir de ahí :

y a partir de ahí :
Sabemos que sec x = 1/cos x; por lo tanto, podemos poner para la integral del enunciado:

y queda resulta integral escrita en el enunciado se resuelve haciendo el cambio :
y queda resulta integral escrita en el enunciado se resuelve haciendo el cambio :
a – bx = t → -b.dx = dt
Con lo cual :

y deshaciendo el cambio:
el ejercicio planteado

y deshaciendo el cambio:
el ejercicio planteado
Para resolver la integral dada en el enunciado, la descomponemos en otras dos mas sencillas :

que resolvemos por separado.
Para la primera tenemos :

Para la segunda hacemos el cambio:

y a partir de ahí tenemos :

con lo que deshaciendo el cambio :

y de ese modo el valor de la integral inicial será

que resolvemos por separado.
Para la primera tenemos :
Para la segunda hacemos el cambio:
y a partir de ahí tenemos :

con lo que deshaciendo el cambio :
y de ese modo el valor de la integral inicial será
Para resolver la integral planteada en el enunciado hacemos el cambio :

con lo que tenemos :

y deshaciendo el cambio:

con lo que tenemos :
y deshaciendo el cambio:
Para resolver la integral escrita en el enunciado, hacemos el cambio de variable:
x = a.t → dx = a.dt
y a partir de ahí :


Para la integral del enunciado, tenemos :

Podemos ver que se tiene una expresión de la forma y'/y cuya integral es ln y ; por lo tanto, la integral nos queda:


Podemos ver que se tiene una expresión de la forma y'/y cuya integral es ln y ; por lo tanto, la integral nos queda:

CONCLUSION
CALCULO
INTEGRAL TOREMA FUNDAMENTAL DEL CÁLCULO ESTA ES UNA INVESTIGACION REALIZADA DE
LOS CONCEPTOS DE INTEGRAL DEFINIDA EN LOS QUE ANTES REPASAMOS ALGUNOS DE LOS
CONCEPTOS IMPORTANTES COMO SON, SUMATORIAS, ANTIDERIVADAS, SUMAS DE RIEMANN Y
LO ESCENCIAL CALCULO DE AREAS.
Sección humorística
En una clase de
matemáticas en un colegio, el profe les esta explicando sobre triángulos a los
niños, pero no demuestran gran interés, asi que saca a uno de los chicos a la
pizarra y le dice que dibuje un punto. El niño lo pinta, y se queda esperando a
que el profe le diga algo más. Pero no, se queda pensando y al final dice :
Pues ya es mala suerte, con la cantidad de puntos que hay en la pizarra y has
ido a dar justo con el que no me sirve.
- ¿A qué distancia esta Nueva York de
Philadelphia?
- Unas 120 millas.
- ¿Y a qué distancia esta
Philadelphia de Nueva York?
- ¡Pues lo mismo, 120 millas!
- No necesariamente.
- De la Navidad al Año Nuevo hay 7 dias, pero del Año Nuevo a la Navidad
hay casi un año.
La fiesta de las f(x)'s (Funciones de X)
En una
fiesta, se habían reunido solo funciones de x. Casi todos estaban
disfrutando de la fiesta, bailando, pisteando, cantando o en el
cotorreo. Pero, pues también fue la función que se quedó sola,
seria y arrejolada en el rincón.
Llegó cos(x) y le
dijo: "ven, integrate a la fiesta", y la solitaria función respondió:
"no gracias, así estoy bien". Más tarde, fue x2 + 2x +1 con
la función arrinconada- "¡Dale!, intégrate con nosotros", pero
volvió a rechazar la función.
Llegó
x+1,
acompañado de otras 2 funciones más y questionó a la función del rincón:
"¡Oye tú!, ¿por qué no te integras?". Y la función dijo: "es que
yo soy ex"
La función ex si se
puede integrar. ʃex = ex
Pero,
tal vez si la función que no se quería integrar fuera x0
entonces al integrarse se convierte en cero, tendría más sentido





No hay comentarios:
Publicar un comentario